Tech Post: A Far Too Detailed Look at Delta-v
Delta-v determines where we can go and what we can do in space, and has a lot of delightful complexity - ergo, prime tech post fodder!
So, the best advice everyone gives you when you run a startup and try to explain the value of what you are doing is to boil it way, way, way down so that anyone can understand it. “Uber for space” or “ChatGPT for biotech” or whatever. For Orbital Arc, the really-boiled-down version is: “Better propulsion, so we can go farther, and do more in space, for much less cost (and someday build space trucks).”
I understand this impulse toward simplification. Really, I do. I promise. (I can sense that if you’ve ever read one of these tech posts before, you don’t believe me.)
Okay, fine. I do understand it, but I don’t like it. I don’t typically find it true that simplification distills ideas or concepts to their fundamental essence. Instead, I usually find that simplifying things misses out on building a deeper understanding of the beautiful complexity of our world. I want the complexity, because that’s the part that’s fun to dig into; it’s the part that you can spend hours working on, hitting a flow state that makes it feel like minutes. It’s where all the discoveries happen, and where all the mysteries lie. In engineering, it’s also the critical means of differentiating between pipe dreams and ideas with real potential.
It is in this spirit, then, that we should talk about delta-v.
[Pictured: A place you can only go with a whole lot of delta-v.]
Delta-v, which just means “change in velocity,” is a measure of how much a spacecraft propulsion system can alter the spacecraft’s velocity before the fuel the spacecraft is carrying is completely used up. I’ve often simplified this by equating it roughly to the driving range of your car on a single tank of gas (or a single charge, for you electric vehicle owners). This is accurate in that delta-v is finite, is based in part on how much fuel you have, and is the determinant of where you can go without refueling, but it is also a “lie we tell to children” in several regards:
Delta-v does not measure distance. It measures maneuvering capacity. In space, the actual distance you can travel very quickly approximates to infinite - you speed up, and there is nothing to slow you down, so you will just keep going forever, either in a loop if you achieve a stable orbit, or in an arc if you exceed escape velocity. It takes maneuvers to make your loop intersect with your target destination, and more maneuvers to stop when you reach that target destination so you don’t just fly right past it. Since that maneuvering capacity is strictly limited by delta-v, that’s the limit on where you can go, and whether you can stay when you get there.
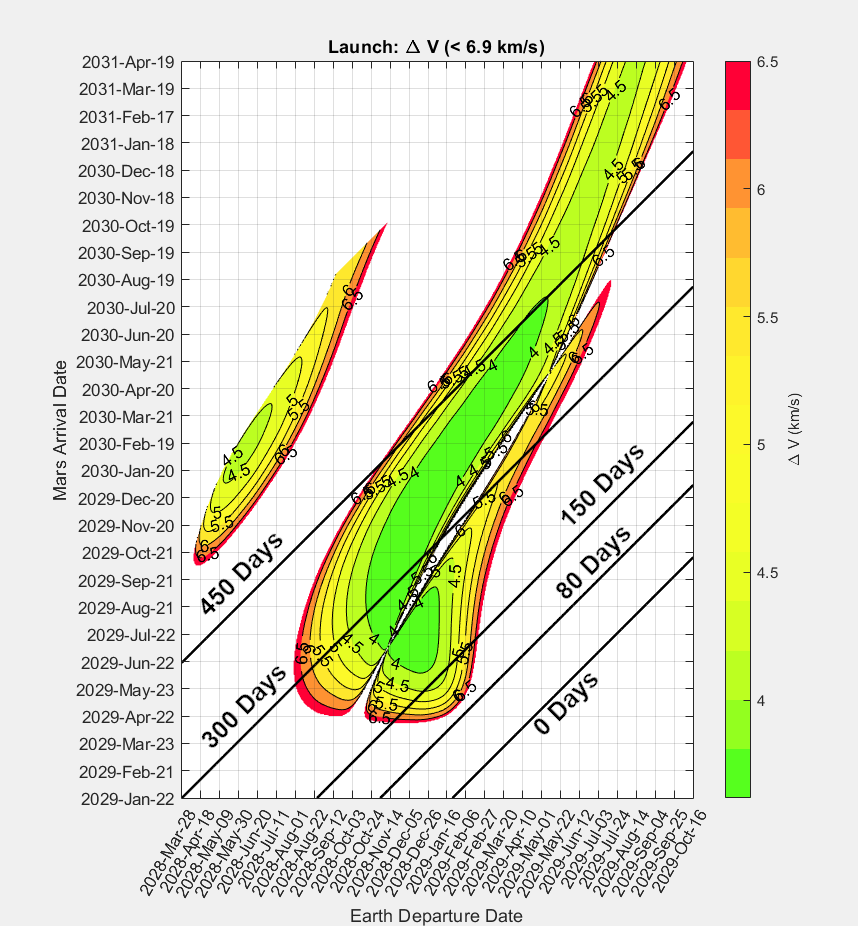
[Pictured: A graph of delta-v from Earth to Mars in 2028 and 2029, depending on departure date and desired arrival date, colloquially known as a “pork chop plot” due to the funny shapes of the colored fields it produces. Notice how certain dates have delta-v below 4 km/s, while all the white space requires more than 6.5 km/s. Also notice the duration lines - if you have 6.5 km/s of delta-v to spend, you can get to Mars in about 90 days, while the most efficient trajectories take at least double that. This is one of the big benefits of ridiculously high delta-v.)
Orbital mechanics makes distances funky. Mars is a moving target; it is half as far away from us as the sun sometimes, and more than twice as far away other times. So, the places a spacecraft can reach with a given amount of delta-v change constantly, and you have to time your acceleration so that your destination gets to where you are going at the same time you do, and the difference in delta-v cost between optimal timing and non-optimal timing is usually huge (see the plot above for an example). This is why launch windows are a thing - our spacecraft have too little delta-v to reach most destinations most times, so we wait (sometimes for years) for planets to literally align to make a mission physically possible with current technology.
Different maneuvering approaches have different delta-v requirements even for the same destination in the same launch window, based on how fast you can accelerate.
If you are orbiting one body, and trying to get to another, your angle of approach to your destination is constantly changing, but you can only thrust along one vector at a time, so if it takes you a significant fraction of an orbit to accelerate, then the correct angle of approach will change while you do the acceleration, and your thrust vector at the start will be off-angle from the correct thrust vector at the end of the burn (in practice, you average it out so that the middle instant of the burn is pointed at the correct angle, and the errors from the beginning and end cancel out, and you end up flying the right direction). This makes the most efficient transfer approach to burn a short, fast burst to get on an intercept course with your destination, and a second short fast burst at the destination to match orbits with it; this approach is called a Hohmann Transfer, and it is typically only possible with chemical rockets.
On the other side of the coin, the longer you take to apply thrust, the more of your thrust is wasted on off-angle error, and the more delta-v you need to get to your destination. Since ion thrusters accelerate slowly, they typically have long burn times, sometimes firing the thruster for months or even years while spiraling outward from a low orbit toward a target, which means that ion engines often need much more delta-v to achieve the same maneuvers as a chemical rocket.
This is partially compensated by the relative velocity at arrival - a “spiral out” trajectory means that when you get to the destination, you have already mostly matched orbits with the destination body, so it takes less thrust during the rendezvous maneuver in most cases. Still, that’s only a partial compensation; Hohmann transfers are still more efficient, requiring as much as 50% less delta-v for some destinations. However, since ion thrusters are generally 6-10x as fuel efficient as chemical thrusters, they still win.
The delta-v you are carrying is also not actually constant; there are a few cheat codes built into the solar system:
The Oberth effect. Your fuel has kinetic energy just like the spacecraft, calculated at KE = 1/2 x mass x velocity squared (0.5m*v^2). The exponent on velocity means that when the spaceship is moving fast, any change in the velocity of the fuel in the tanks (such as, say, shooting it out the back for thrust) yields an exponentially larger change in kinetic energy than the same exhaust velocity would achieve from a standstill. This means (weirdly) that the faster you are already going when you apply thrust, the more delta-v you get out of it. If you can set it up so your spacecraft falls deep into a gravity well and you fire thrusters at the very bottom of the well, you can get an exponential bonus to delta-v as a result, because you converted a ton of potential energy to kinetic energy in your fuel, and then capitalized on it before the orbit converted it back to potential energy.
Gravity assist maneuvers. Approach the planet from behind, so that it is travelling away from your approach vector as you arrive, and let its gravity pull your spacecraft forward while the planet itself “runs away.” The spacecraft gets pulled for much longer than it would otherwise, accumulating velocity. As long as you set the trajectory up so that you don’t fly straight out ahead of the planet afterward (where backward drag would cancel this effect because the planet “keeps up” with the spacecraft as it tries to run away), you can set things up to keep some of the velocity you accumulate, and can change direction almost for free.
Aerobraking. When you arrive someplace that has an atmosphere, you can dip the spacecraft into it, and wind resistance will slow you down. This can make landing on the atmosphere-encrusted body almost delta-v free, can help adjust a trajectory, and can also help with insertion to a target orbit over the body - basically, as long as you slow down enough on the first pass to avoid flying past the body entirely, you can keep flying through the drag-inducing upper atmosphere over and over, and lower your orbit a little bit each time. Eventually, you do need to apply thrust to stabilize/circularize the orbit, or you end up crash landing on the planet though. However, you do have to build your spacecraft so it doesn’t fall apart in the breeze.
[Pictured: The Tyranny of the Rocket Equation. Y-axis is delta-v, X-axis is the mass ratio, meaning “mass when full / mass when empty.” Think of it like a fraction; if the mass ratio is 10, then the empty mass is 1/10th the full mass, so the spacecraft is 90% fuel. “V-exit” is exhaust velocity, for which ISP is a proxy; note how higher exhaust velocity yields higher delta-v. For context, best exhaust velocity we can achieve with chemical propulsion is about 4500 m/s.]
Delta-v is strongly constrained by the rocket equation (see above). Adding more fuel means you are carrying more mass, and each unit of incremental fuel therefore provides exponentially less and less incremental delta-v benefit. The exponential decay here puts a hard cap on delta-v (barring use of the cheat-codes described above) for any given spacecraft dry mass at any given ISP (which is specific impulse, or fuel efficiency). This makes higher ISP super valuable, as it increases the delta-v cap, but there are some complications worth understanding:
The “delta-v cap” isn’t actually dependent only on ISP; if you could make the entire spacecraft only of fuel, then more fuel would always give you more delta-v, regardless of your ISP. In fact, if you had a specific payload and spacecraft mass, the same would be true - more fuel would always be more delta-v. In both cases, adding more fuel gives you exponentially diminishing returns, but there are still returns. The thing that causes a “cap” on delta-v is that the mass of your power and propulsion systems typically scales at least a little bit with your total fuel consumption - usually you can’t burn the fuel tank for thrust, and even though fuel tank volume increases with radius cubed while surface area (the main driver for tank mass) increases with radius squared, increasing tank mass eventually adds more dead weight to slow you down than the fuel from added tank volume adds acceleration. That’s the actual cap for delta-v at any given ISP. Higher ISP = higher cap, but lower tank mass also has a surprisingly large impact on maximum possible delta-v because it impacts the onset point of the scaling factor that ultimately blocks any further incremental delta-v gains.
The situation described in “a” above is how it works for chemical propulsion, where power is stored as chemical potential energy in the fuel. If you use electric propulsion, you also need a way to make your power, which is another thing that scales up in mass in tandem with power. In electric propulsion you have the advantages of much higher ISP, and the ability in many systems to pick your ISP. We could actually design the thruster to push ISP as high as we want. However, a linear increase in ISP requires an exponential increase in power, which, in turn requires an increase in the mass of your power supply. As with fuel tanks, power supply mass eventually grows faster than the benefit of higher ISP can compensate. This makes power efficiency in the thruster incredibly important, and mass efficiency in the power supply equally so. In effect, there is a maximum practical ISP that depends on the thrust per watt metric of the thruster and on the watts per kilogram metric of the power supply. Going higher than the ISP max is not that hard with current technology, but it is stupid because the added power supply mass will more than negate any gains from added efficiency. That max ISP in turn sets a max delta-v for any given payload due to the tank mass scaling constraint.
We’ve touched on this above, but it’s worth it to emphasize: Delta-v is not only forward momentum, it is also the limited capacity of your brakes. If you want to stop anywhere that doesn’t provide you an atmosphere for aerobraking, you have to spend delta-v to slow down. This makes orbital rendezvous missions at any place that lacks an atmosphere MUCH more expensive than just flying by, and also why sample return missions are MUCH more expensive than rendezvous missions. To go and come back, you accelerate to fly out, decelerate to stop at the destination, accelerate again to come home, and decelerate again when you get here (though Earth has an atmosphere so you can often aerobrake for the last one). That might take 3-4x as much delta-v as just doing a flyby, and since fuel requirements scale exponentially, that means 9-16x as much fuel, even before you account for the incremental fuel needed to move added dry mass from bigger fuel tanks and power supplies. It gets impossible quickly, which is why we call it the “Tyranny of the Rocket Equation.”
So, putting all this together, how much delta-v can we reasonably achieve, and how much cost should you expect for it?
[Pictured: The Dawn spacecraft, flying toward Ceres.]
The most delta-v ever applied by any spacecraft flying under its own power was about 11,500 m/s; this was the Dawn mission that visited the asteroids Ceres and Vesta, running at up to 3,100s of ISP, on 425 kg of xenon propellant, plus 100 kg of hydrazine propellant for higher thrust maneuvers and station keeping/pointing while orbiting the target asteroids; dry mass was 747 kg, of which about 20 kg was scientific payload, so fuel mass fraction was ~41.3%, and payload mass fraction was ~1.6%. The flight also used a Mars gravity assist, which added some velocity and helped change direction, but we won’t count it in our total. If we consider the hydrazine to be just dry mass, and assume that Dawn had drained its xenon tanks completely, it actually could have put out about 12,890 m/s of delta-v just on its ion engines.
Working with modern technology, we can improve on Dawn’s delta-v performance. For example, the solar arrays for Dawn totaled 126 kg to provide 10 kW of power at Earth (1.4 kW at Ceres); that’s about 79.4 W/kg. We now have solar arrays that produce 300 W/kg, and may soon get to 1000 W/kg. At 300 W/kg, the solar array mass could have been cut to about 33.3 kg, which would allow an extra 92.7 kg of fuel, which would have allowed Dawn to reach 16,552 m/s of delta-v. Adding 28% more delta-v by adding 21.8% more xenon fuel has just as much to do with decreasing dry mass as with increasing fuel. If you just reduce the mass of the spacecraft by shrinking solar panel mass, and don’t add fuel, you still have 14,170 m/s of delta-v, capturing about a third of the benefit even with no additional fuel.
If we then add in thrusters like the ones we are developing, you can do better still. The NSTAR thrusters on Dawn massed 8.2 kg each, with PPUs massing 13.3 kg each (3 thrusters, 2 PPUs aboard for redundancy), with tank mass of 19 kg for compressed xenon. Only one thruster ran at a time, consuming up to 2.56 kW to provide 90 mN of thrust at up to 3100 seconds ISP (Note, sources vary on ISP max, so we’re just using Wikipedia numbers for this example).
Our thrusters, by comparison, will mass less than 500 g, and at 3100 ISP and 90 mN, our thruster would require only 1.53 kW, about 40% less power. Our PPUs are also expected to mass about 5 kg for a 2 kW thruster, and using solid fuel allows about a 75% reduction in tankage mass compared to composite carbon fiber overwrap tanks. Put all that together, and we shave 23.1 kg from thruster mass, 16.6 kg from PPU mass, 14.25 kg from tank mass, and an additional 13.4 kg from solar arrays (sticking with our earlier adoption of 300 W/kg arrays), a total mass reduction of 65.8 kg, which, if we shift this mass to fuel, will bring total delta-v up to 19,528 m/s.
There is one slightly misleading element here - this math just adds fuel to add delta-v, keeping thrust constant. It makes a good way to compare two propulsion systems and illustrate how much difference mass reductions can really make, but you would never do this in reality because it would also add flight time; in this case, it would now take our modified Dawn spacecraft 6.3 years to burn through all its fuel at full power. Also, by reducing our solar panels, we ensure we will not have full power when we reach the asteroid belt - sunlight there is too dim, and even the real mission ran only about 1 kW to thrusters for the whole second half of the trip, which is why it took so long.
So, in practice, if we were planning the Dawn mission today with Orbital Arc thrusters, we would not cut back on solar panels. Instead, we would leverage the better power efficiency to run the thrusters at higher power and longer to get more thrust and shave a couple years of flight time (with associated reduction in ground operations cost), and we would probably double or triple the payload mass allotment to do more science and get much more total value out of the trip.
And, that’s the whole point of what we are doing: Move more stuff through space faster, for lower cost. See, I can oversimplify!